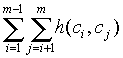
The Effect of the Average Hamming Distance of the Initial Population on the Convergence Rate of a Population Run
As with most dynamic systems, the terminal fitness of a population of solutions which have been operated upon by the principles of Genetic Algorithms (GAs) is undoubtedly affected by the initial state of that population. The terminal fitness of a population is the highest fitness of the final population of a run. This paper aims to shed light on the effect of the average Hamming Distance between members of the starting population on the terminal fitness of a population.
Maximum Hamming Distance
As we know, Hamming distance is the number of differing bits between two binary chromosomes. For example, the Hamming distance between 111100 and 111111 is 2. Total Hamming distance is computed by the following forumla:
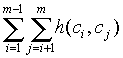
where h(ci,cj) is the Hamming distance between two chromosomes ci and cj of a population C = {c1,c2,...,cm}. In the case of two chromosomes the maximum total Hamming distance of the population is the chromosome length. However when we compute total Hamming distances in populations larger than two, then the maximum of the sum is not so obvious. For the purposes of this paper it is necessary to be able to compute the maximum of the sum of Hamming distances of a population given the population and chromosome size.
Since Hamming distance is computed on a bit by bit basis (values on any other loci have no effect on the Hamming distance of the present locus) it follows that the maximum Hamming distance of m chromosomes n alleles long is equal to n times the maximum Hamming distance of m chromosomes with only one allele.
When dealing with chromosomes of length one, it quickly becomes apparent that the sum of the Hamming distances is equal to the number of 1’s times the number of 0’s. Let us assume that the population size, m, is evenly divisible by 2 such that m equals x + x. The ratio of 1’s to 0’s that we desire can be derived by finding the maximum of (x + k)(x – k). This is achieved exactly when k is equal to 0.
Therefore, the maximum Hamming distance (H) for an even population size is given by:
H = (nm2)/4
With some thought we find that the general formula for maximum Hamming distance is:
H = n * floor(m/2) * (floor(m/2) + mMod2)
Note that
(nm2)/4 >= n * floor(m/2) * (floor(m/2) + mMod2)
Experiment 1
Chromosome size: 16 bit binary string.
Fitness Function: f(x) = x2.
Mutation Rate: .001 per allele.
Crossover: Two-point.
Population size: 16.
Number of Runs: 128.
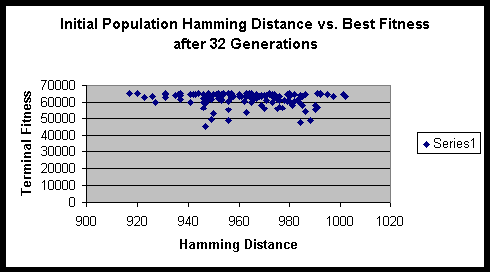
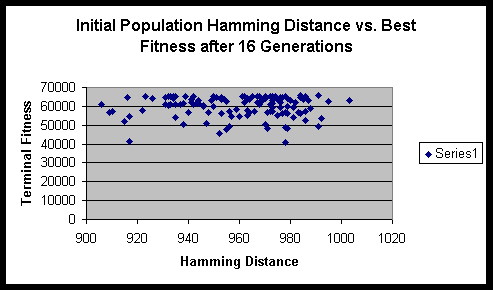
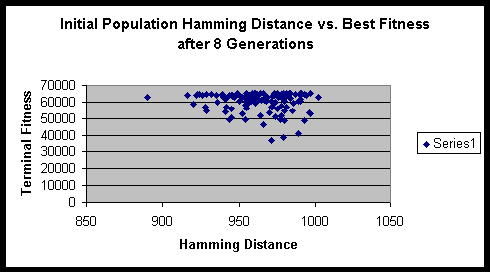
Chromosome size: 16 bit binary string.
Fitness Function: f(x) = the sum of all 1’s.
Mutation Rate: .001 per allele.
Crossover: Two-point.
Population size: 16.
Number of Runs: 128.
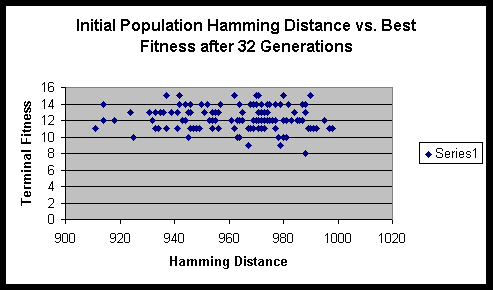
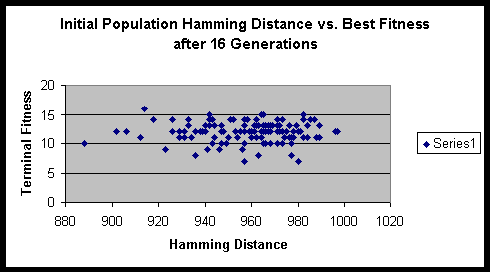
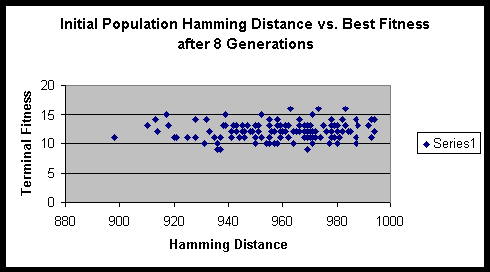
Analysis
From the formula that we derived above, we can compute the maximum sum of Hamming distances for this experiment to be 1024. Fortunately / unfortunately it works out such that as the population size gets large the ratio of the initial Hamming distance sum to the maximum Hamming distance sum approaches 1. Though one might think that a population size of 16 is quite small, it actually has sufficient numbers to eliminate significant fluctuations in the initial Hamming distance sum.
Both experiments suggested that there is minimal variance of terminal fitness of a population when the initial Hamming distance sum is in the range of 900 to 1000. On a side note, the hitch-hiking of defective alleles is apparent in these experiments. Of the several hundred runs, only a very small minority ever achieved the maximum fitness possible.
Future Work
Clearly there are many more roads to travel in order to fully explore this problem. Varying mutation rate, population size, chromosome size, and crossover methods are all good starts. A necessary first step would be to artificially bias initial Hamming distances so as to get a better idea of how a population is affected by very little diversity.